Multiple-pattern search problem

A common problem in processing textual input is searching for occurrences of patterns known prior. This can be solved on CPU as well as on GPU.

All measures of CPU performance were taken on an Intel i7-6700HQ processor using 8 threads. The measured GPU was Nvidia GeForce GTX 1050 Ti.

CPU approach

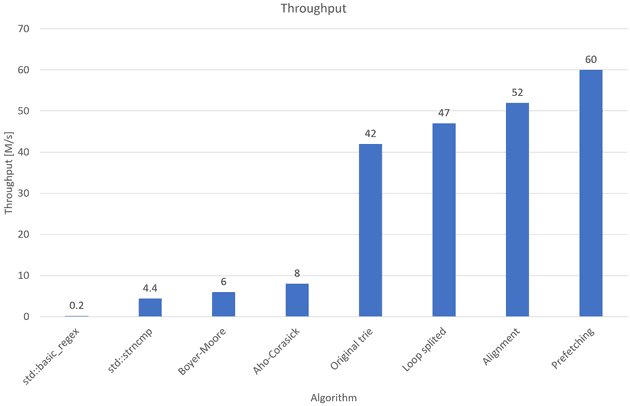
The first approach was to use regular expression functions from the Standard Template Library¹. While it was easy to implement, the preprocessing throughput was at the level of 200 thousand searches per second. We have never considered regular expressions to be the final solution, however, the mentioned result will serve as a performance baseline for subsequent approaches. It will also show the difference between generic solutions and specialized algorithms.

The next used method was the naive string-search algorithm applied for each pattern. In this case, STL also offered its implementation². This time, the throughput was significantly better with a number of about 4 million input lines per second.

Afterwards, we tried to solve the problem by using the Boyer–Moore algorithm. It is described by Boyer et al.³. The algorithm is available in the STL since C++17, however compiler used in tests didn’t support C++17, therefore we had to implement it ourselves. This solution gave us a throughput of 6 million matches per second.

The previously mentioned algorithms are designed to search for a single pattern. All of them had to be applied for each pattern separately, whereas the following methods search for all patterns simultaneously. While comparing results, it should be taken into account that in our tests there were only 5 patterns, thus more complex requirements of a system might increase the gap between single and multi-pattern search.

The last algorithm we have tested was the Aho–Corasick algorithm described by Aho et al.⁴. The increase in performance was significant, by 33%, resulting in a throughput of 8 million logs per second.

The comparison of all benchmarked algorithms, including the ones mentioned afterwards, is shown in Figure 3.

GPU approach

After establishing a baseline for comparison we moved to a GPU implementation and started considering possible solutions.

We could not have used the Aho–Corasick algorithm from the previous solution, due to efficiency issues created by additional traversing caused by suffix links. In the SIMT execution model, the smallest atomic group of 32 threads, called a warp, must execute the exact same instruction. In the case of suffix links in the algorithm, a single thread might block execution of the other 31 threads. Apart from that, reading from 32 distinct areas of memory can cause memory dependency, which results in warp throttling, and performance decreasing.

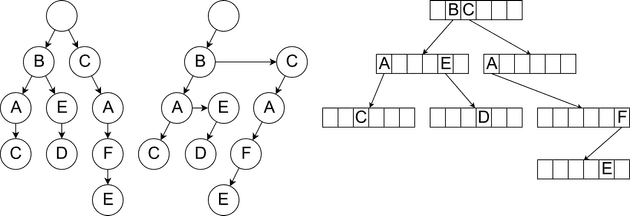
We decided to abandon Aho–Corasick algorithm and try with a prefix tree known as a trie⁵. A trie is a data structure that allows storing and searching strings efficiently. The idea behind a trie is simple. Each node represents a character in a string. Each child of a node represents a possible next character, one that matches a single (or more) of the strings stored in the trie. There are two common ways to implement a trie: as a left-child right-sibling binary tree and as a tree with arrays as nodes. The overview of those implementations is presented in Figure 1.

Figure 1. Possible trie representations. From left to right there are: an abstract view of trie structure; left-child right-sibling binary tree; tree with arrays as nodes.

Left-child right-sibling binary tree, also known as a doubly chained tree, represents nodes as linked lists. Each node has two links, the left one pointing to a child, and the right one pointing to the next sibling. To check if a specific node has a child containing a given character we must:

1. Go through the left link.
2. Check if the child contains the wanted character, and if it does not, go through the right link until a wanted child is found or the list ends.

While this implementation is space efficient, going through next siblings causes throttling of all threads in a warp, each time one of them traverses through the, possibly numerous, nodes.

The second implementation, which uses arrays as nodes, avoids this problem by allowing access to each child of a node in constant time. It is done by treating characters as indices, based on their ASCII value. A disadvantage of this implementation is increased memory usage. It’s especially painful on GPU where amount of fast access memory (shared memory⁶) is limited. Additionally, patterns with short common suffixes cause wasting a majority of allocated memory to be wasted.

Trie construction

We decided to go with the letter implementation as it seemed more suitable for GPU execution and memory model. To make the implementation more efficient we adjusted a tire to a test case by applying following optimizations.

One of the assumptions made was searching only for alphabetic characters and ignoring their case. It allowed us to minimize each node array from 256 to 26 elements by storing only characters in a range a-z. While traversing through a trie, only alphabetic characters are considered, with uppercase letters being transformed to lowercase. Their ASCII order will be used as indices for a node array.

Next, we considered patterns that we were looking for. As we had only few patterns to look for, and they tend to branch out quickly in a trie, we decided to optimize in this direction. We identified every branch that does not split until its end. Each such branch got compressed by storing it contiguously in memory as a suffix of a pattern, terminated with the null character and the output key of this pattern. This improvement has two relevant outcomes:

1. Compressed branches take 26 times less memory as we store only a single character instead of an array of 26 elements.
2. Since the suffix is stored contiguously, we can read a chunk of data instead of single characters. It results in fewer memory reads and improves performance.

Our approach has a small drawback, namely differing sets of instructions for the threads traversing through nodes and the threads traversing through suffixes. However, when a thread finds a dead end, it simply stops and waits for the other threads to finish. In our case, it is common for most threads to finish quickly, and usually the only one that lasts is the one that finds a pattern.

The described trie has features that allow efficient GPU computation. However, it has to be in the form of a raw byte array, in order to be passed and used on a GPU. To achieve this, we transform the trie in the following way:

• In the raw byte array, all nodes are stored contiguously, each of them represented as an array.
• Afterwards, suffixes of patterns are stored contiguously.
• Values in the node arrays represent offsets from the beginning of the byte array, with 0 signifying that the character is not a child of the node.
• If the child is a suffix instead of a node array, then the most significant bit is set in the offset.

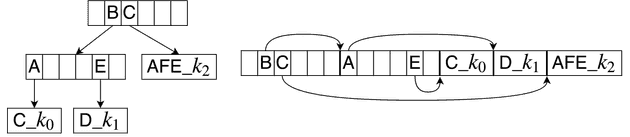
The creation of the tries is performed on the CPU for each defined set of pairs of patterns and keys. It is done only once, during the start of the application. Afterwards, the trie, in the form of continuous array, is transferred to the GPU. Figure 2 presents the same compressed trie in two representations.

Figure 2. Two representations of a compressed trie. On the left, a compressed trie with links, on the right, a trie as an array. k_n represents the output key of a pattern and the symbol _ represents the null character.

A measured throughput of a trie constructed this way was 42 million input lines per second.

Code optimization

As the last step, we searched for optimization within the code of a trie search. Traversing a trie isn’t an easy task to cooperate on from a warp perspective. Thus, we were able to gain some performance by applying some common optimization techniques.

The first optimization was splitting the main loop of the search function. The initial function had a form in which all threads loop until they reach the end of a trie. Since we had two types of nodes, array and compressed, we had to keep a flag that indicated how to behave. It causes for warp to split, since some threads were still going through arrays while others were already checking compressed nodes.

We split the loop into two. The first that goes through node arrays until it reaches the end or compressed node. The second loop was going only through compressed nodes. This split gave us a significant increase in performance, to 47 million input lines per second.

The next optimization was data alignment of compressed nodes. Compressed nodes were aligned to 4 bytes which allowed us to utilize a whole read to shared memory. Instead of going byte by byte we fetch 4 characters at once to a register and iterate over them in a separate mini-loop. The optimization boosts throughput to 52 million input lines per second.

The last applied optimization was prefetching. It was the easiest and yet the most significant improvement in the code. We added a line that loads data from shared memory to a variable before the main loop and adjusted the loop. The few lines changes gave us throughput of 60 millions input lines per second.

Figure 3. Comparison of Multiple-pattern search algorithms. Loop splitting, Alignment and Prefetching optimizations are described in other blog texts.